This will be the first in a series of articles that dive into the advanced applications of implied volatility. You can read the first series of articles about IV in this category: Implied volatility. That series looked into the implied volatility and some of its special characteristics (Ranking, drop after earnings etc.). UPDATE: Checkout part 2: Edge of Skew Rank – Part 2
In the upcoming articles we will talk about volatility skew, and more specifically – volatility skew rank.
What is volatility skew?
Implied volatility is usually arranged in a “smile”. That is that the further the option is from the money (where the underlying last price is) the higher the Implied Volatility (IV). When plotted on a chart – it looks like a smile:
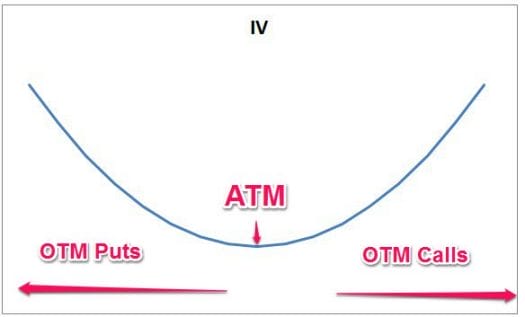
The skew is the measure of the “slant” on this smile. Options practitioners use this slant (or skew) to measure if the options are pricing a bullish move or a bearish move.
How to read IV Skew?
There are many ways to measure options skew. Some of the ways:
- Measure 25 delta put minus 25 delta call
- Measure 5% OTM put minus 5% OTM call
- Check ATM calls vs. OTM calls, or ATM puts vs. OTM Puts.
- And more.
While the calculation is different and will yield different results, when analyzed compared with historical data, most calculations will yield a similar conclusion. This is because the most common use is for, comparing the current value with the past value to find abnormalities, and not calculating profit according to them.
Here are examples of bullish skews and bearish skews; notice that these are rough examples, and in practice, there are many other forms:
Bullish:

Bearish:
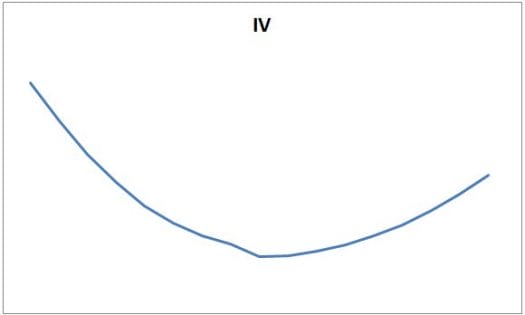
I hope that from these examples, it is clearer why this indicator is called “skew”:
- When comparing the examples with each other (and from the first example at the beginning), we can see that in the bullish example – the IV is higher the more we move to the right (OTM calls are more expensive). That means that the market prices these options more expensively, probably because of many players assume an upmove.
- Similarly, in the bearish example, the puts are priced more expensively.
Since options are usually priced currently, we can say that if one side is priced more expensively that there is greater fear in the market to move in that direction.
What doesn’t skew measure?
As we saw, skew measures IV between options. It doesn’t measure:
- Skew doesn’t measure if IV is high or low.
- Even if the skew is bullish or bearish, it doesn’t indicate a trade – we need to compare those values to the past in order to reach an actionable signal.
- Each asset has its own skew and characteristics. Usually, puts are priced more expensively, even if the market is in a bullish trend.
Read more about the edge in volatility here.
Volatility Skew Rank
Volatility skew Rank was designed to standardize different skew values and compare them with their historical value. This is so a trader/investor can get all the information he/she needs in one glimpse. The standardization helps overcome the disadvantage of the skew and the fact that you need to compare the skew values to themselves. We wrote an in-depth guide about IV Percentile here.
How to find options by Skew Rank
- Skew Rank – The current skew of the stock (-25 delta put vs. +25 delta call) vs. its value over the last year.
- Put Skew Rank – The current put skew of the stock (-25 delta put vs. ATM put) vs. its value over the last year.
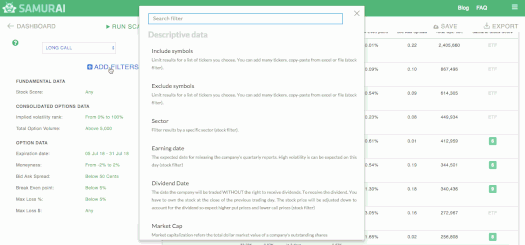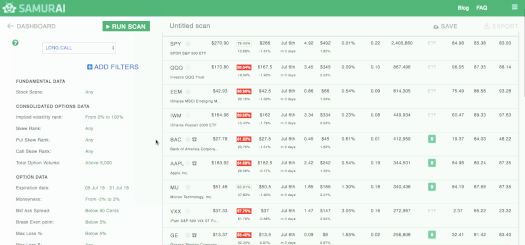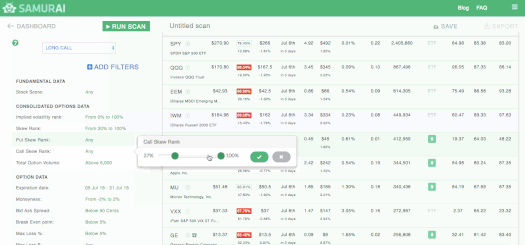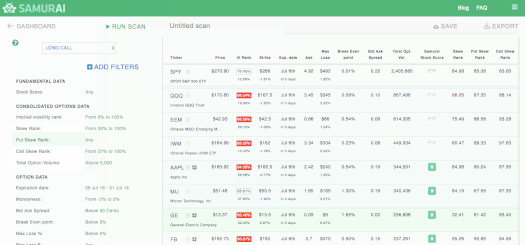
- Call Skew Rank – The current skew of the stock (ATM call vs. 25 delta call) vs. its value over the last year.