In the OptionSamurai Scanner, we use IV Percentile to compare the IV of different stocks and call it “IV rank” as we think it is more intuitive to understand. We know that other market players (such as Thinkorswim or tastytrade) use those two terms differently. To avoid confusion, this post will explain the difference between the two.
IV Rank and IV Percentile
IV percentile is a measure of implied volatility vs. its past values. It measures how many of the past IV values are lower than the current IV value. An example best explains this: If IBM IV percentile is 34% – It means that the current IV value is higher than 34% of previous values (and, of course, lower than 66% of them).
IV Rank is also a measure of implied volatility vs its past values, but it looks only at the highest and lowest values. The formula is:
[IV – Lowest_IV]
[Highest IV – Lowest IV]
If IV values are not too extreme and the look-back period is long enough (about a year), then values will be very similar. However, we feel that the IV percentile is a better indicator and is more robust (albeit harder to calculate).
This simplified example will show the difference between the calculations:

In the above example, we see four past values. Now we have a new value – 15, and we will calculate both the IV percentile and IV Rank:
- When calculating the IV rank, we can see that 15 is exactly the middle between the highest and lowest IV values (10&20), and Thus the rank will be 50%.
- When we calculate the IV percentile, We can see that 15 is larger than three of past values out of the four values in our set so that the rank will be 75%.
We feel that the IV percentile is a better indicator, and we use it, even if we call it “IV rank,” which we feel is the more intuitive way to understand it.
We ran backtests to show the edge of the Implied Volatility Percentile and the Edge of the Skew Rank. Check out our articles.
How to scan for IV rank in OptionSamurai:
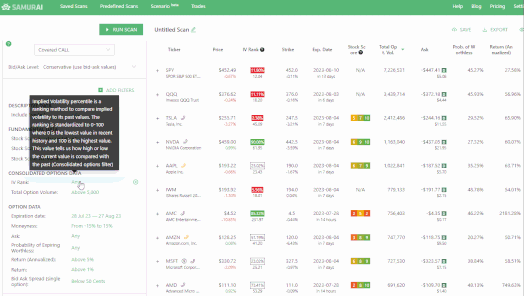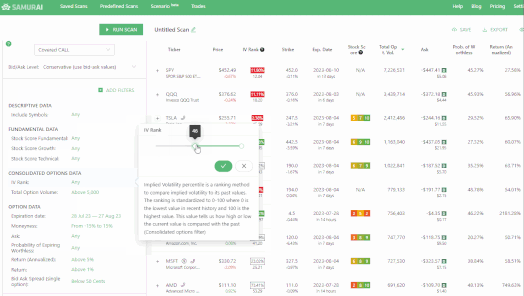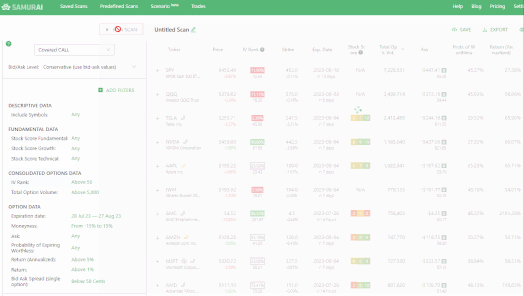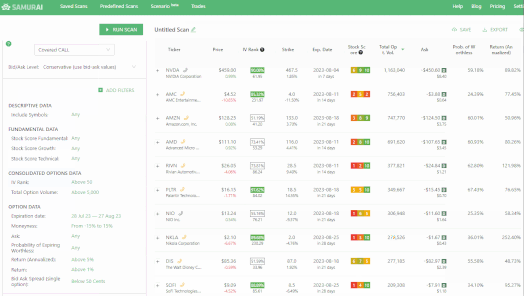
-
- We have a complete volatility suite in Option Samurai. Read the knowledge base here.
(Originally published on Jan 29th, 2015, and updated since)


In wich level of IV rank or IV percentile do you prefer to write options and buy options?
Hey Edgar,
The IV is only one of the parameters I use when deciding to trade, so it depends on the system. If the main reason for trade will be the IV I think I would like it o be extreme, but also for a long period of time. so maybe above 80, but for several days before I sell the option… same for buying, usually under 20. This is a bull market so I think now you can even wait longer for low IV, so require it to be below10 for over a week.
Again, I personally take into consideration more than just the IV.
Im agree with your point of view, even if we are taking about advance strategies the thechnical must match with all..
Thank You so much dear Shogun!
what can i say this is a great platfrom
Thanks!